遥感应用模型课程要求做一些文献阅读,抽了一篇是建筑物提取的benchmark数据集上SVM,ELM和FCN三种算法的比较分析,为了完成作业做一些简单的整理和记录.

文章内容

本文旨在比较三种流行的监督机器学习模型(SVM,ELM,FCN)在仅使用高分辨率栅格数字表面模型(DSM)数据的建筑物提取任务上的性能,均使用像素级的目标检测策略,在ISPRS的"Test Project on Urban Classification, 3-D Building Reconstruction, and Semantic Labeling"项目提供的benchmark上进行测试.

benchmark 指的是一种测试标准.用于评估系统,硬件或软件的性能.通过运行一系列预定义的任务,可以比较不同系统之间的性能差异.

文章工作流

本文的实验分为三个步骤: 数据预处理,模型训练和模型评价. 主工作流

数据预处理

数据处理工作流

数据集是航空图像和激光扫描仪数据组成的集合,分别用于城市目标检测(urban object detection)和三维景观重建(3D building reconstruction).本文使用的原始影像是基于此得到的DSM影像.该数据集有包含三个城市区域:

数据描述 数据源 数据描述
Vaihingen an der Enz DGPF 呈现出相对较小的中欧村庄的特征,有许多独立的建筑和小型的多层建筑,包含了略有不同的城市机理.
Postsdam DGPF 代表了一个典型的中欧历史城市,建筑街区大,街道窄,聚落结构密集.
Toronto - 展示了典型的现代北美大都市的特征,高低层建筑混合,包括投射出相当大阴影的高层建筑群.屋顶结构和街道的形状呈现不同程度的复杂性.

由于本文使用的三种方法均需要监督分类,因此需要根据任务需要首先对影像进行标注.即需要建立对影像建立二值分类: 建筑与非建筑. Vaihingen an der Enz和Postsdam两个区域的二值掩膜是从数据集提取的,而Toronto的数据集是直接从已有的矢量数据集得到.

接着对数据源进行同化.由于不同地区使用不同的遥感平台进行观测,因此三个城市数据分辨率不同,分别为5cm/pixel,9cm/pixel和25cm/pixel.本文使用最近邻插值将其统一至36cm/pixel由于提升算法性能.

原则上接着需要对数据进行清洗等操作.不过由于benchmark数据质量高,建筑与非建筑像素比例接近1:1,地物对象边缘清晰,且噪声,缺失值和异常值等极少,故不做单独说明. 在完成与处理后,按照经验比例进行训练集/测试集的划分.

模型训练

模型训练工作流

本文使用数据集提取的建筑分类结果对三个模型进行训练,该部分将在下文"算法基础"中展开.

模型评价

模型评价工作流

使用测试集对三个模型进行检验,检验的指标有:

名称 公式 含义
Sensitivity \(\frac{TP}{TP+FN}\) 在所有实际为正的样本中正确被模型识别为正的比例,反映模型对正类样本的识别能力.
Specificity \(\frac{TN}{TN+FP}\) 在所有实际为负的样本中正确被模型识别为负的比例,反映模型对负类样本的识别能力
PPV(Precision) \(\frac{TP}{TP+FP}\) 在所有被预测为正的样本中实际为正的比例,评估预测为正的样本是否准确
NPV \(\frac{TN}{TN+FN}\) 在所有被预测为负的样本中实际为负的比例,评估预测为负的样本是否准确
F1 score \(2\cdot\frac{PPV \times Recall}{PPV + Recall}\) Precision和Recall的调和平均
MSE \(\frac{1}{N_{\text{pixels} } }(\text{imageref} - \text{imageout})^2\) 预测值与实际值之差的平方的平均,衡量模型预测值与实际值的偏差
MCC \(\frac{TP\times TN - FP \times FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)} }\) 用于衡量二分类问题中模型性能的指标,在类别不平衡情况下是一个更可靠的衡量指标

具体结果将在下文进一步讨论.

算法基础

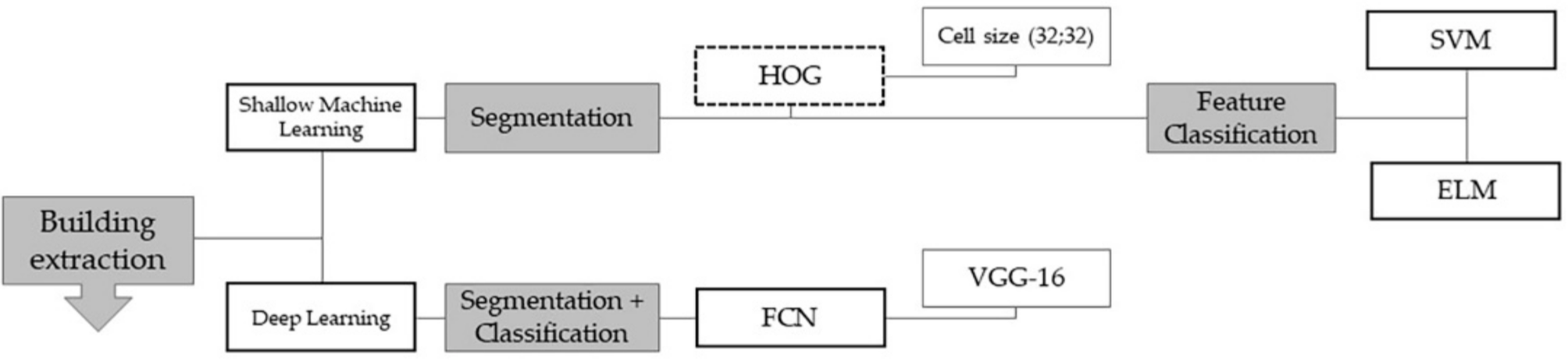
本文使用的三种算法各有特点,可以从多个角度分类: - 浅层学习与深度学习: SVM,ELM & FCN - 凸优化与神经网络: SVM & ELM,FCN - 分阶段处理与端到端处理: SVM,ELM & FCN

从这三个角度出发比较,FCN作为深度学习算法需要更高的训练成本,SVM作为凸优化方法具有更高的可解释性,FCN作为端到端的算法同时完成了语义识别任务中的分割和识别.对应地,SVM和ELM作为分类算法并没有回答如何进行语义分割的问题,本文对这两个分类器引入的图像分割特征描述子是HOG.以下将先对HOG-SVM和HOG-ELM模型进行介绍,再介绍FCN算法.

特征描述子-HOG

基本思想

定向梯度直方图(Histogram of Oriented Gradients, HOG)是一种用于图像处理的特征描述子,通过计算和统计图像局部区域的梯度方向直方图来构成特征. 其基本思想是: 即使不精确知道相应的梯度或边缘位置，局部物体的外观和形状通常也可以通过局部强度梯度或边缘方向的分布来很好地表征. ### 算法流程 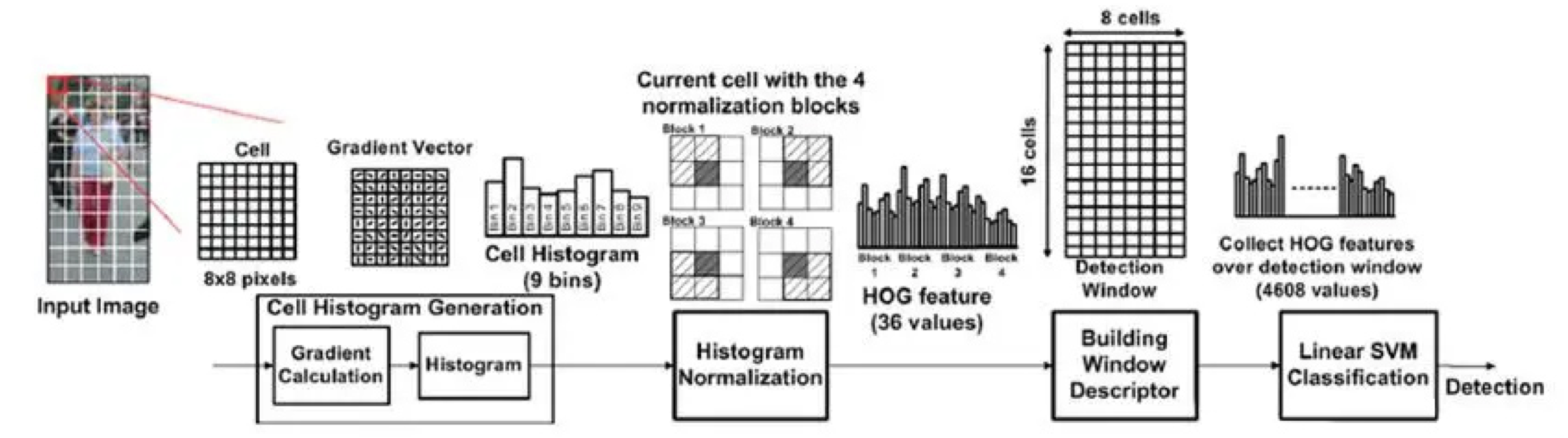HOG工作流

特征的构建可分为六个步骤: 1. 将图像分为若干小区域(cell) 2. 对于每个cell根据需要进行Gamma校正和灰度化等操作 3. 计算cell里每个位置的水平梯度和垂直梯度并计算梯度方向和梯度大小. 4. 以\(20^\circ\)为宽度设置9个bin,并将cell里梯度大小依据梯度方向加权统计到各个bin中. 5. 将相邻\(n \times n\)个cell合成block,并将得到的\(9n^2\)个特征进行标准化. 6. 将block窗口以cell为单位在图像中滑动从而构建整个图像的特征描述子.(由于block有重叠相当于over detection)

算法实现

计算图像梯度

原始文献(Dalal et al, 2005)指出最简单的梯度算子\([-1,0,1]^\intercal\)具有最好的效果,因此对于\((x,y)\)位置的像素值\(H(x,y)\),其水平梯度\(G_x(x,y)\)和垂直梯度\(G_y(x,y)\)为

\[ \begin{aligned} G_x(x,y) &= H(x+1,y) - H(x-1,y) \\ G_y(x,y) &= H(x,y+1) - H(x,y-1) \end{aligned} \]

计算得到梯度大小\(G(x,y)\)和梯度方向\(\alpha(x,y)\)为:

\[ \begin{aligned} G(x,y) &= \sqrt{G_x(x,y)^2 + G_y(x,y)^2} \\ \alpha(x,y) &= \arctan (\frac{G_x(x,y)}{G_y(x,y)}) \end{aligned} \] 其中\(0 \leq \alpha \leq 180^\circ\).

加权统计梯度信息

将\([0,180^\circ)\)分为\([0,20^\circ),[20^\circ,40^\circ),\ldots,[160^\circ,180^\circ)\) 9个bin并左对齐,使用序列\(l_k = (20k)^\circ,k = 0,2,\ldots,8\)表示,并特别地记\(l_9\)表示区间\([0,20^\circ)\).则位于\((x,y)\)的点其加权统计方式为 \[ \begin{aligned} S_k(x,y) &= G(x,y) \cdot (\alpha(x,y) - l_k) \\ S_{k+1}(x,y) &= G(x,y) \cdot (l_{k+1} - \alpha(x,y)) \\ \end{aligned} \] 其中\(l_{k}\leq \alpha(x,y) < l_{k+1}\),\(S_k(x,y)\)表示\((x,y)\)位置对第\(k\)类的梯度贡献.

在block中归一化梯度直方图

对每个block中\(9n^2\)个向量使用L2范数归一化: \[ v = \frac{v}{\sqrt{||v||^2_2 + \epsilon^2} } \] 其中\(\epsilon\)是一个小的正则量.经验的,若以\(2\times 2\)为范围合并cell. 归一化可以实现对边缘,光照和阴影等干扰的压缩,可以进一步提高泛化能力.

支持向量机(SVM)

支持向量机(Supporting Vector Machine, SVM)是一种二分类模型,其基本模型定义为特征空间上的间隔(margin)最大的线性分类器,学习策略是使间隔最大化,最终可转化为一个凸二次规划问题的求解.

SVM大家都很熟悉了,只做简单介绍. ### 具有最大间隔的线性分类器 一个线性分类器的学习目标便是要在 n 维的数据空间中找到一个可以将特征空间将不同样本分离的超平面(hyper plane),表示为:

\[ w^\intercal x + b = 0 \]

将其记为\((w,b)\),则样本空间中任意点\(x\)到超平面\((w,b)\)的距离可写为

\[ r = \frac{w^\intercal x + b}{||w||} \]

记待分类的数据点为\(x\),类别为\(y\)取值\(\pm 1\),则若超平面\((w,b)\)能将训练样本正确分类,为了表示方便令 \[ \begin{cases} w^\intercal x_i + b \geq +1, y_i = +1 \\ w^\intercal x_i + b \leq -1, y_i = -1 \end{cases} \] 其中使不等式取等的数据点称为支持向量.两个异类支持向量到超平面的距离之和为\(\gamma = \frac{2}{||w||}\),\(\gamma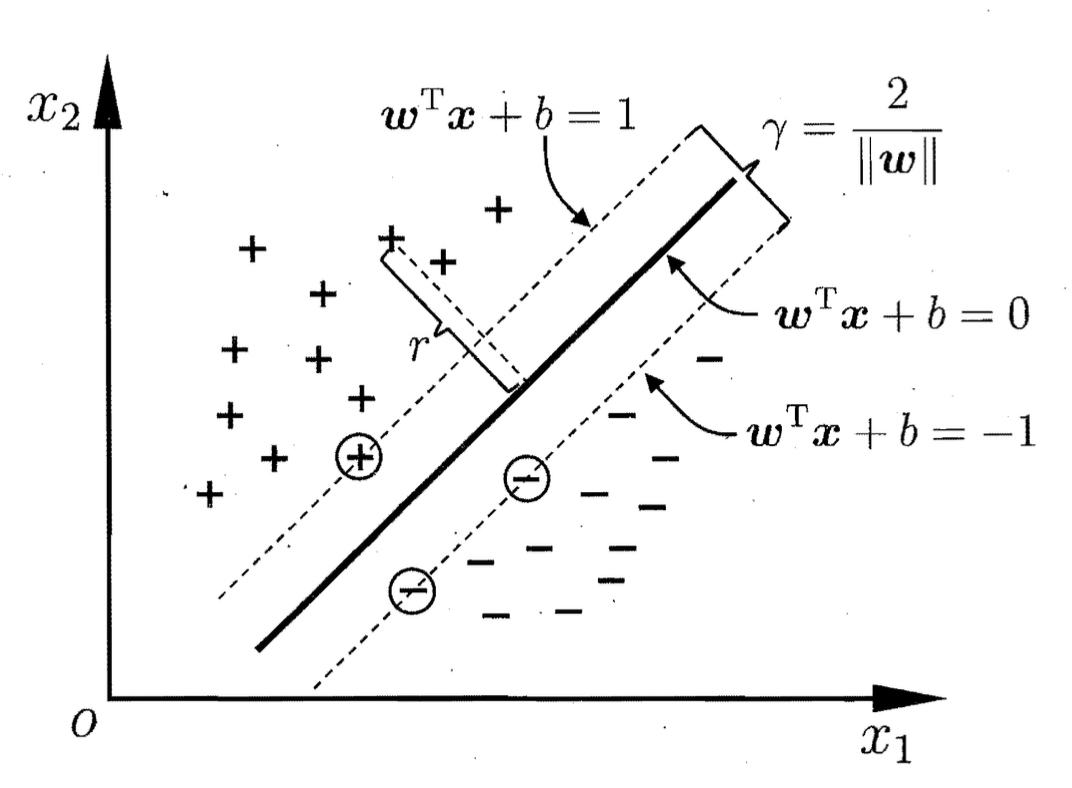\)表示间隔.

优化目标可表示为:

\[ \begin{aligned} \max_{w,b} &\frac{2}{||w||} \\ \text{s.t.}& y_i(w^\intercal x_i + b)\geq1,i = 1,2,\ldots,m \end{aligned} \]

该方程可显然等效为 \[ \begin{aligned} \min_{w,b} &\frac{1}{2}||w||^2 \\ \text{s.t.}& y_i(w^\intercal x_i + b)\geq1,i = 1,2,\ldots,m \end{aligned} \] 此为SVM的基本型.进一步讨论不在此处展开.

极限学习机(ELM)

极限学习机(Extreme Learning Machine, ELM)模型的网络结构与单隐层前馈神经网络(SLFN)一样,但不使用后向传播(BP)算法进行参数学习,而采用随机指定输入层权值和偏差,通过广义逆矩阵理论计算得到输出层权重的方式.

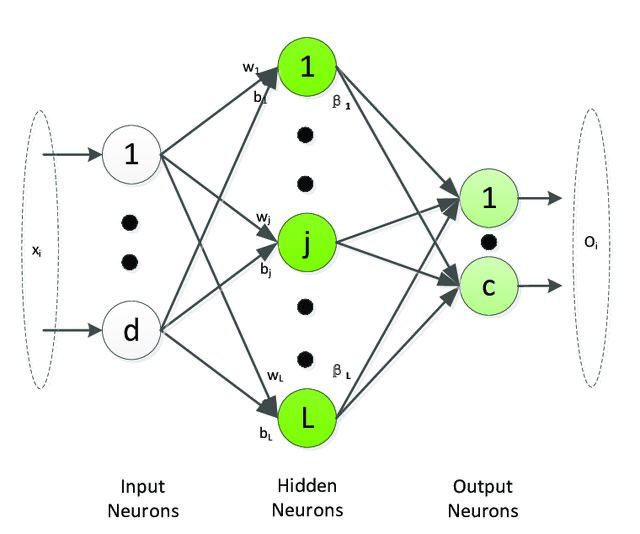
ELM网络

从输入层到隐藏层之间是全连接，记隐藏层的输出向量为\(H(x) = [h_1(x),\ldots,h_L(x)]\),其中\(h_i(x)\)的计算方式为

\[ h_i(x) = g(w_i,b_i,x) = g(w_i x + b_i), w_i \in R^D,b_i \in R \] 其中\(g(w_i,b_i,x)\)是一个满足ELM通用逼近能力定理的非线性分段连续函数,如Sigmoid函数,Gaussian函数等.那么对于给定数据集\(\{x_i,t_i \mid x_i \in R^D,t_i \in R^m,i = 1,2,\ldots,N\}\),该隐层的输出映射矩阵\(\displaystyle \mathbf{H}\)为

\[ \mathbf{H} = \begin{vmatrix} h(x_1) \\ \vdots \\ h(x_N) \end{vmatrix} = \begin{vmatrix} g(w_1,b_1,x_1) & \cdots & g(w_L,b_L,x_1) \\ \vdots & \ddots & \vdots \\ g(w_1,b_1,x_N) & \cdots & g(w_L,b_L,x_N) \end{vmatrix} \]

ELM通用逼近能力定理描述了这么一件事: 如果训练样本够大以至大于训练参数则损失函数可以取到0,否则对于任意给定的\(\epsilon\)总存在一个样本规模使得训练损失能小于\(\epsilon\).具体的数学证明请查看论文.

此时我们随机指定\(\mathbf{w}\)和\(\mathbf{b}\),我将\(\displaystyle \mathbf{H}\)形容为"网络在当前样本上的一个指定状态",在指定后我们唯一要训练的参数集只有\(\mathbf{\beta}\)即隐层到输出层的连接权重.加入正则化参数,目标函数表示为:

\[ \min ||\beta||^2 + C||\mathbf{H}\beta - \mathbf{T}||^2 \] 其中\(\mathbf{T}\)是训练数据的目标矩阵.

实际上这个ELM的目标函数可以超级复杂,此处仅给出一个简单的形式(岭回归).

那么\(\beta\)最优解\(\beta^*\)为

\[ \beta^* = \mathbf{H}^+\mathbf{T} \] 其中\(\mathbf{H}^+\)为矩阵\(\mathbf{H}\)的Moore–Penrose广义逆矩阵.在\(\mathbf{H^\intercal H}\)非奇异时就是熟悉的正交投影基\(\mathbf{H}^+ = (\mathbf{H^\intercal H})^{-1}\mathbf{H}\).通用地,\(\mathbf{H}^+\)可使用SVD计算,此处不展开讨论.

全连接卷积神经网络(FCN)

全连接卷积神经网络(Fully Convolutional Network, FCN)顾名思义是一种卷积神经网络(Convolutional Neruo Network, CNN),其与典型的CNN在网络结构上的关键区别是将CNN最后的全连接层换成了卷积层.因此我们先简要介绍CNN,再分析FCN网络结构的变化带来了什么,并对FCN的一些实现进行说明.

CNN-图像语义识别的利刃

典型的 CNN 由3个部分构成:

  • 卷积层(Convolutional layer) 负责提取图像中的局部特征.
  • 池化层(Pooling layer) 大幅降低参数量级(降维),并提升模型泛化能力.
  • 全连接层(Fully connected layer) 类似传统神经网络的部分,用来输出想要的结果.

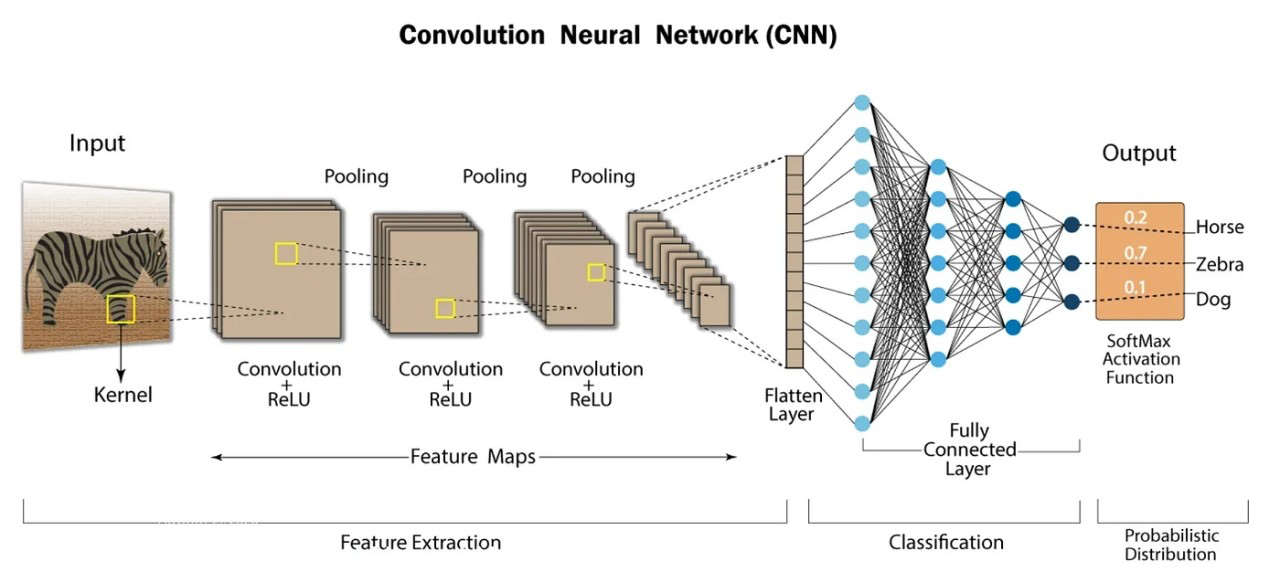
相比于原始的全部由全连接层构成的多层感知器(Multilayer Perceptron, MLP), CNN对卷积的引入对图像语义识别带来了许多帮助:

  1. 大幅降低了输入全连接层的数据量.
  2. 更好识别局部特征
  3. 每一个局部使用同一套参数(卷积核),降低训练成本.

进一步的细节请查阅CNN有关文章.

卷积原理

我觉得上图对卷积运算的演示非常值得一提,要注意卷积操作在运算时是把一个局部的全部特征维同时输入一个卷积核,而一个卷积核在滑动完成后得到的是新图像的一个特征维,也就是有多少个卷积核新图像就有多少特征维度.

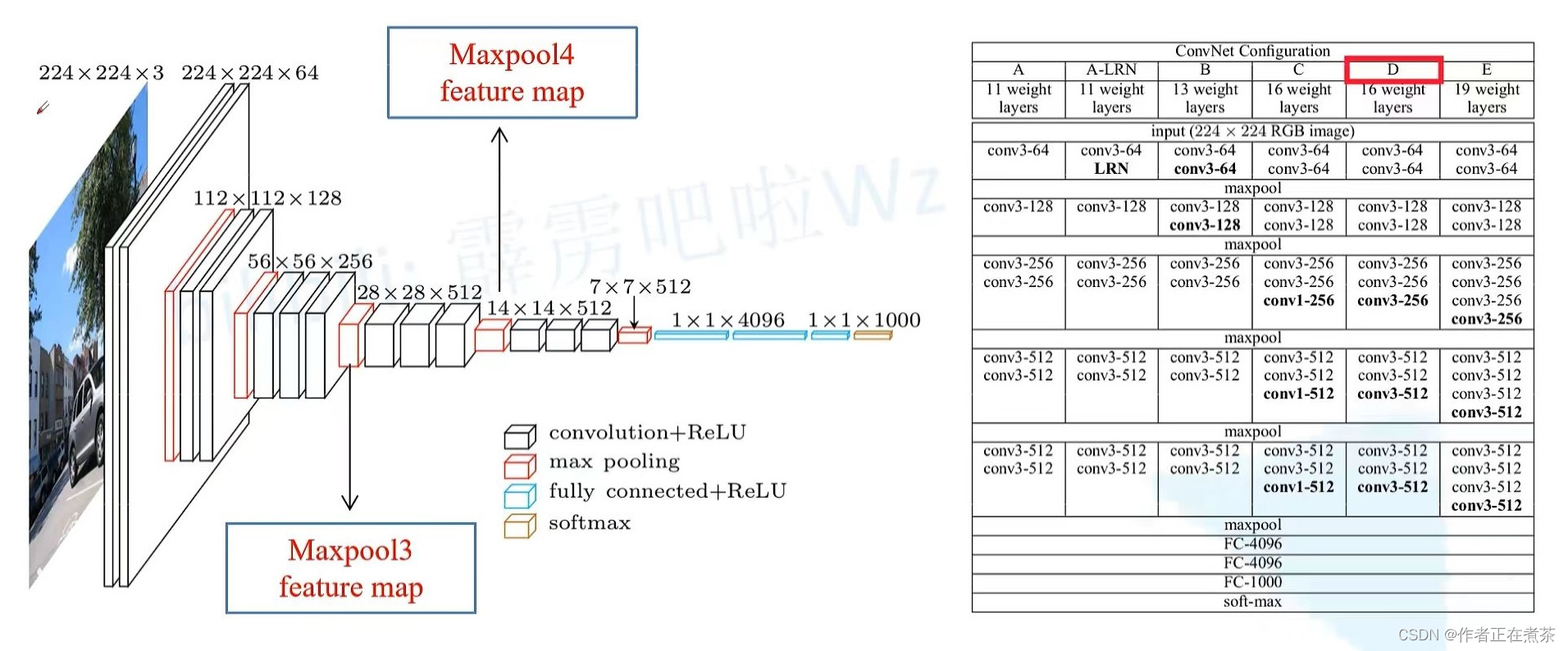
在这个思想上,AlexNet首先证明了其在图像学习上的强大威力,而VGG网络结构则是整理了AlexNet的思路,提供了一套"将卷积运算打包分类"的范式,而(本文的)FCN正是基于VGG16构建的.

第一次实现端到端的图像语义分类

观察上图CNN的训练过程我们可以发现,CNN网络最终得到的结果是"某一像素所属的类别",我们还需要根据像素排列将预测结果拼起来,那么是否存在一种方式使得我得到的结果就是一张与输入图像大小相同的图像,其像素值包含的就是其分类信息? FCN就做到了这件事.解决方式异常简单: 将CNN网络中的最后一部分全连接层换成了一组新的卷积层--转置卷积. 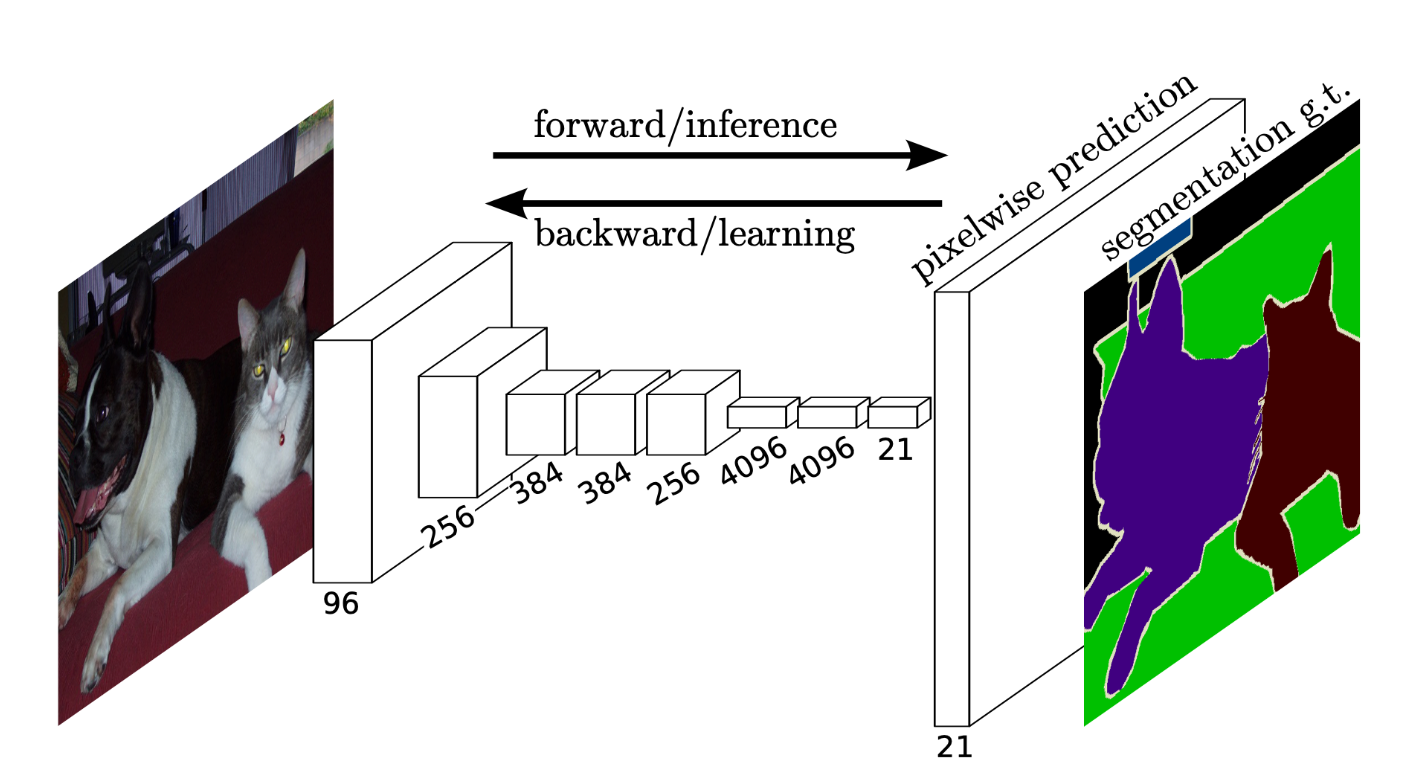注意,转置卷积也是卷积,其思想类似于"既然我要将图像扩大到\(n\times m\)大小,而卷积操作会使得图像变得更好,那我先将图像padding到比目标图像更大,再用一次卷积操作使得得到的图像尺寸是我要的结果."

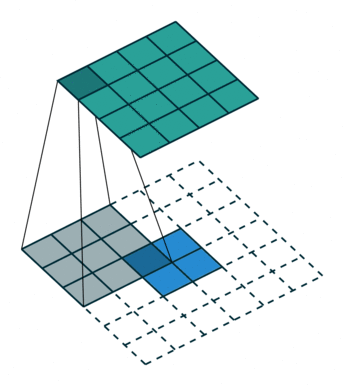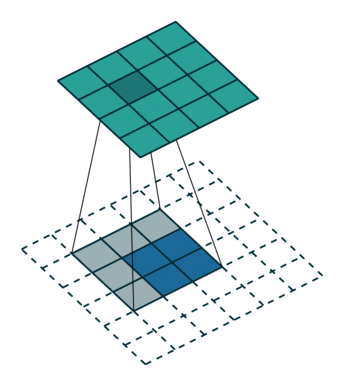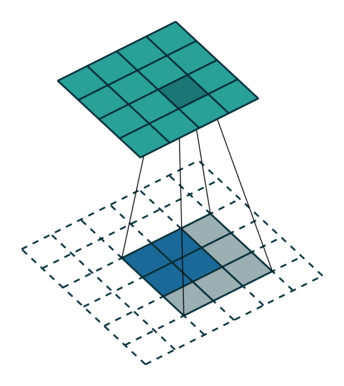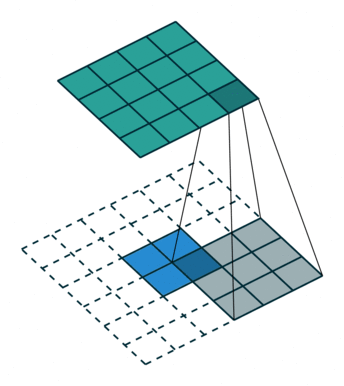
转置卷积示意图

这样的操作与unpooling和unsampleing不同,不需要记录max pooling过程中使用的值的位置,相应地,卷积核也需要进行训练,具体的训练方式可查阅相关文献.

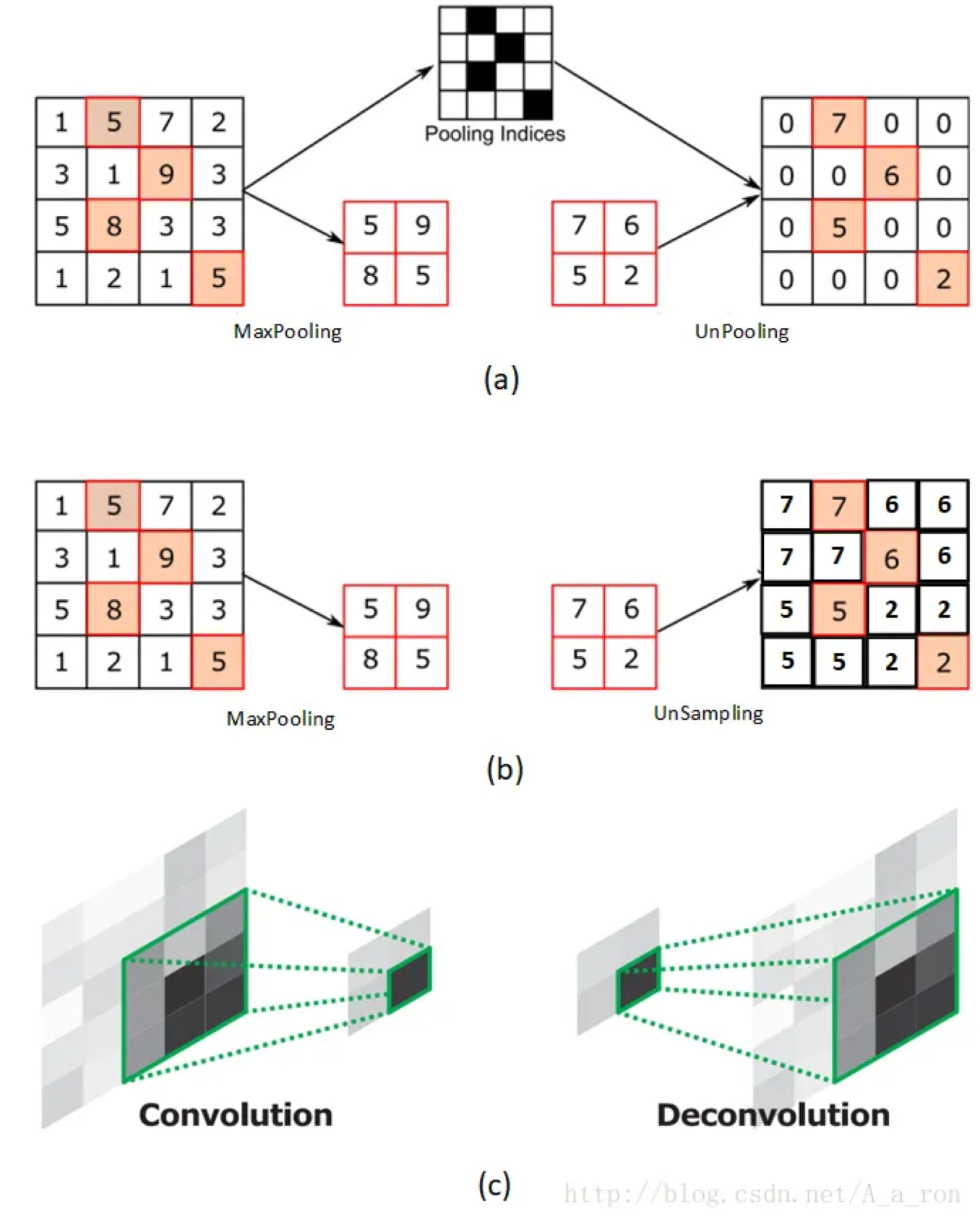
然而,在比如使用卷积将输入图像缩小到原尺寸的\(\frac{1}{32}\)的情景下,让转置卷积一次性上采样32倍(FCN-32S)实在太"为难"他了.因此FCN-16S和FCN-8S网络则使用中间过程进行融合从何缓解了上采样时倍率过大的问题,很好地提高了模型精度. 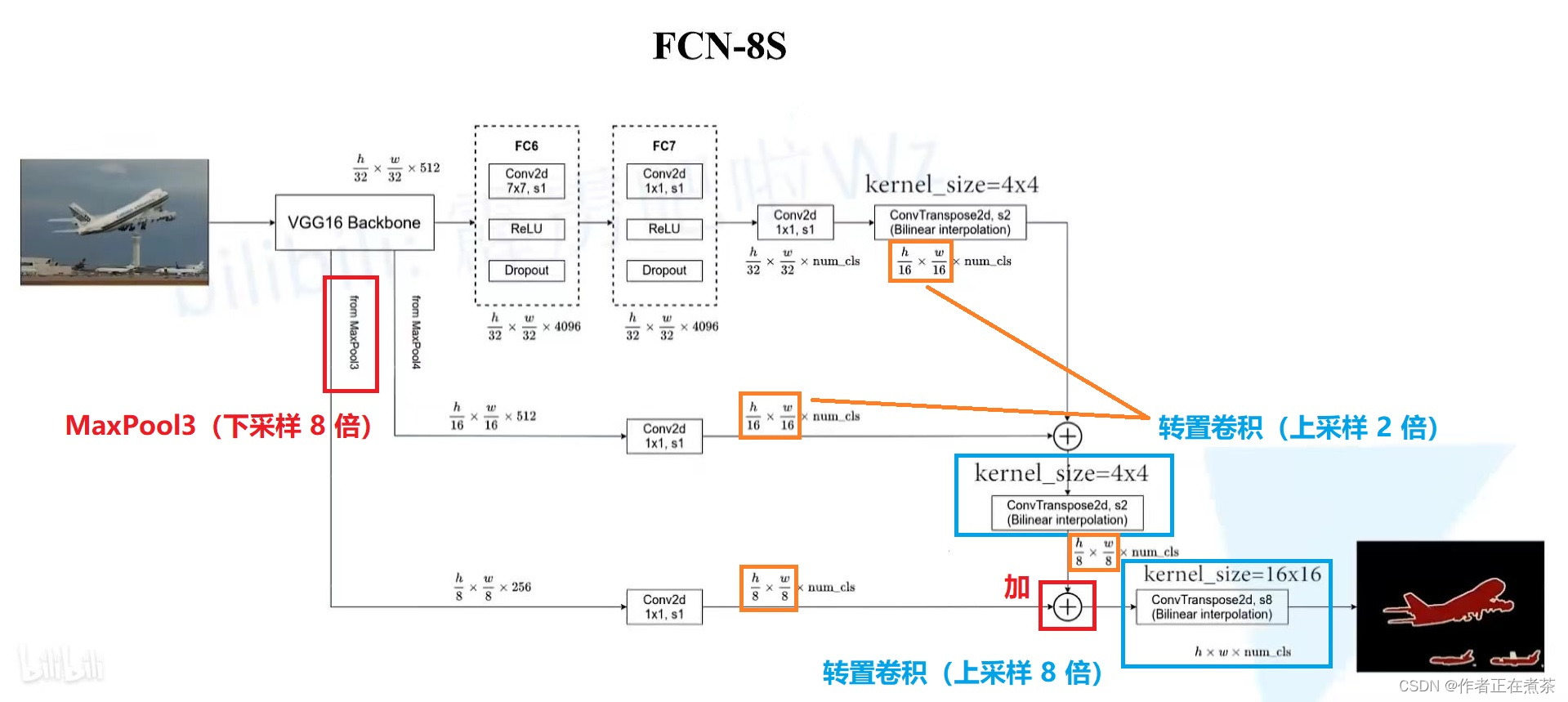具体的数学推导请查看相关资料. # 讨论 ## 三个模型的性能评价

论文中给出的指标: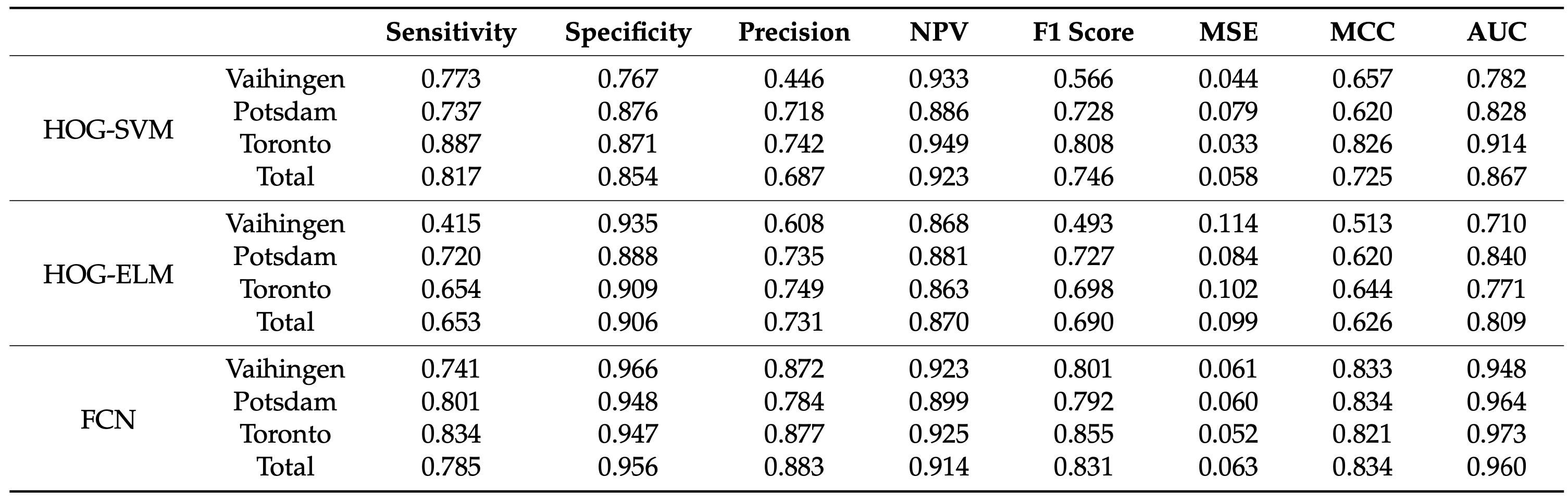

  • 在Vaihingen测试集FCN模型的MCC值明显优于其余模型,与ELM分类器相比,SVM更倾向于检测建筑像素,其Sensitivity更高,但Speicificity较低.相对于非建筑像素的指标没有发现明显差异.
  • 在Potsdam测试集,SVM和ELM分类器在Sensitivity方面表现出相似的结果,FCN模型优于HOG-SVM模型;考虑MCC时,这种差异变得更大.
  • 在Toronto测试集,HOG-SVM和FCN模型的MCC值显著高于HOG-ELM模型,后者的Sensitivity和NPV较低.

综合考虑,基于FCN的深度学习方法是最优方法,因为无论城市背景如何其都能实现良好的分类,两种基于 HOG 的模型的性能都受到研究的城市环境的影响,性能的下降在 Vaihingen 地区表现尤为明显.在考虑该文章给出的三种不同城市的背景下,这种方法相较于其他两种方法产生的结果更好,ELM和SVM模型则分别存在低估和高估建筑物像素的问题，影响了检测的准确性.

模型名称 模型评价
HOG-ELM 倾向于低估建筑物像素导致较高的漏检率.在Vaihingen和Toronto区域,ELM的检测效果不佳,小型建筑和特定建筑类型(如庭院)的内部结构被误判.
HOG-SVM 在Toronto和Vaihingen的一些场景倾向于高估建筑物像素,表现为较高的误检率.尤其在Vaihingen区域由于误检率高导致预测的建筑物像素过多.
FCN 在所有测试子集中,FCN模型在预测建筑物的位置和大小上表现最佳,与真实地面数据的对应关系最为吻合,显示了更高的检测准确性.

总之,本文的结论是非常直觉的,"The bigger, the better".值得注意的是,轮廓和边界的不准确是基于深度学习分割的一个缺点.同时,虽然本文选取了三个不同的城市区,但均集中在欧美地区,训练样本依然受限. ## 本文提出模型在我国建筑物提取任务中的潜力 介绍一篇本文的引用,该文从城市建筑密度模式和土地利用混合模式两个角度比较了东西方城市形态的差异,为模型的迁移提供参考. 该文分析的研究区如下图所示,包含东亚和东南亚区域的典型城市.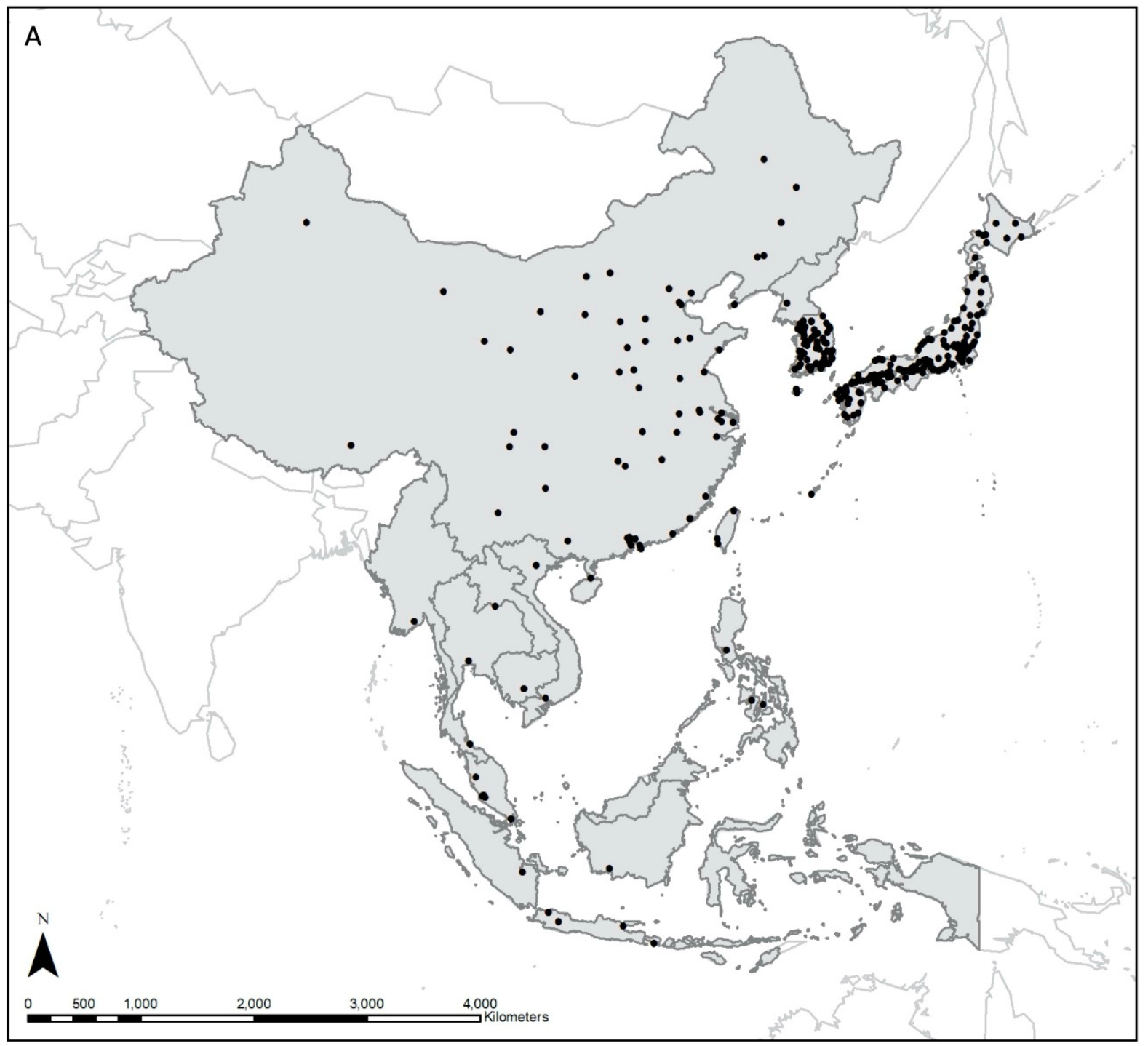

其中提到土地混合利用中东方和西方城市的差异主要体现在东方国家城市土地以混合利用为主可分为水平,垂直和时序上的混合利用.其中以居住与就业的土地混合利用组合为典型.例如一般而言台北市包含56种土地利用类型和12个土地利用区,每个土地利用区允许10种以上类型.

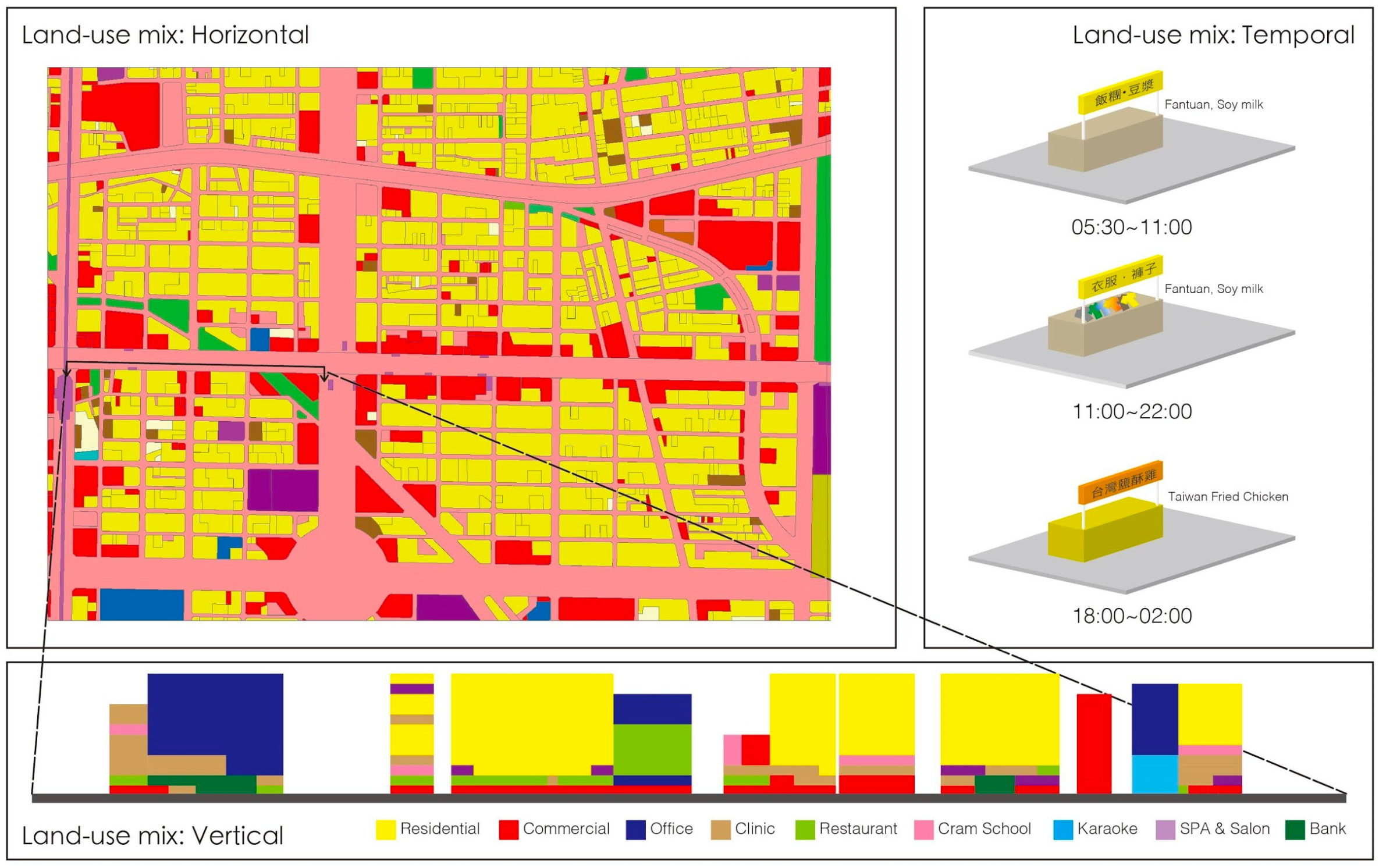
个人感觉这对我们的启示是这对DSM的重建和建筑提取的一致性造成挑战,由更复杂的垂直结构和单个建筑及其相邻建筑形成的更复杂的纹理引起.

FCN模型在时序建筑物提取中的应用潜力

从地理学的视角出发,FCN已经证明了其对建筑物的"模式"的提取能力,那么其对建筑物的"过程"的提取能力呢? 本文是学长做的研究,之前看过就打算一起聊一下.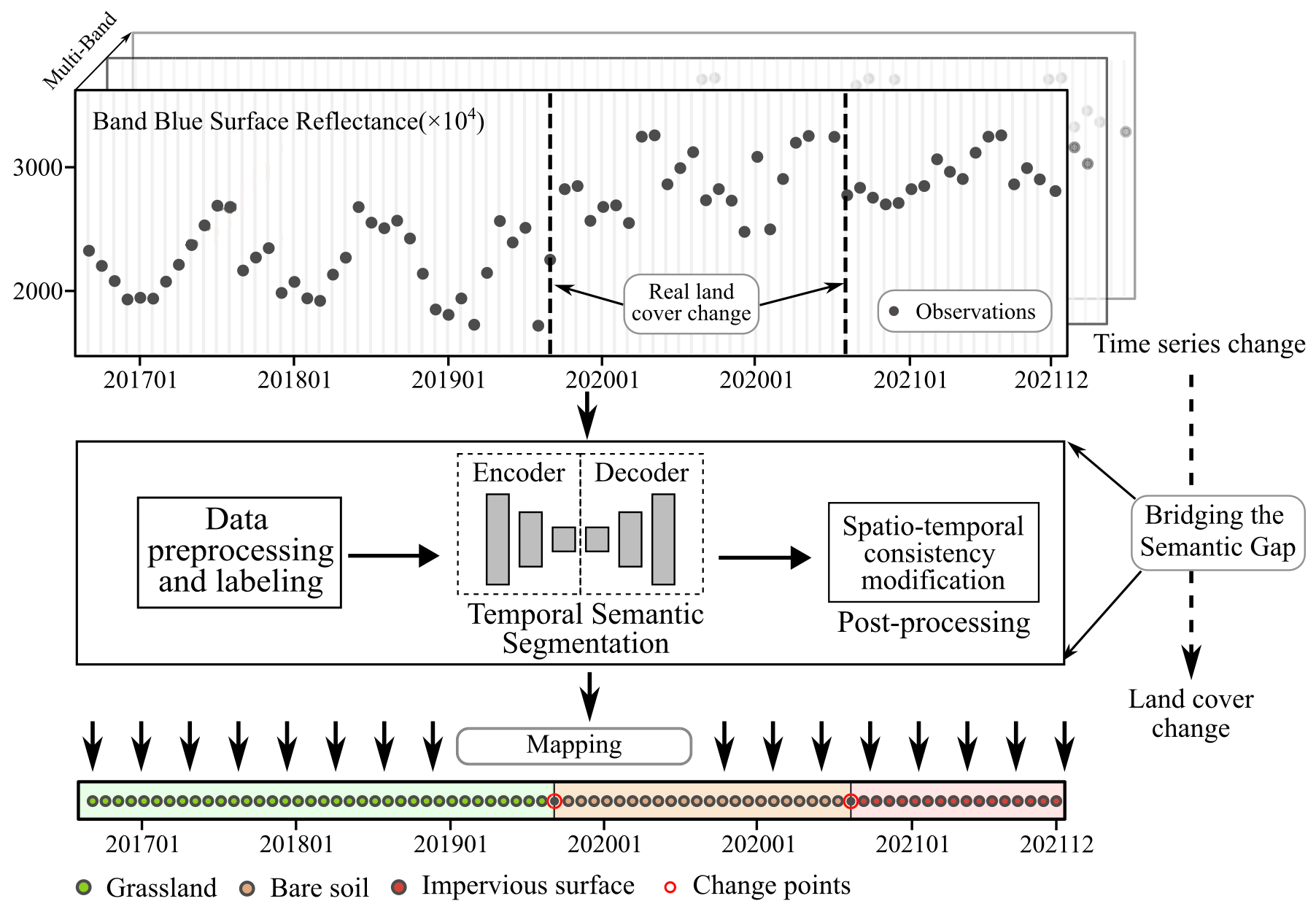

在城市发展的后期阶段,为了满足更复杂的遥感时间序列解释需求,需要弥合像元变化和语义变化之间的“语义鸿沟”.这里的像元变化利用卫星光学遥感影像提取,语义变化特征表示为逐时相的土地覆盖类型变化.因此,本文的思路是使用FCN对单一像元长时序的特征进行学习.

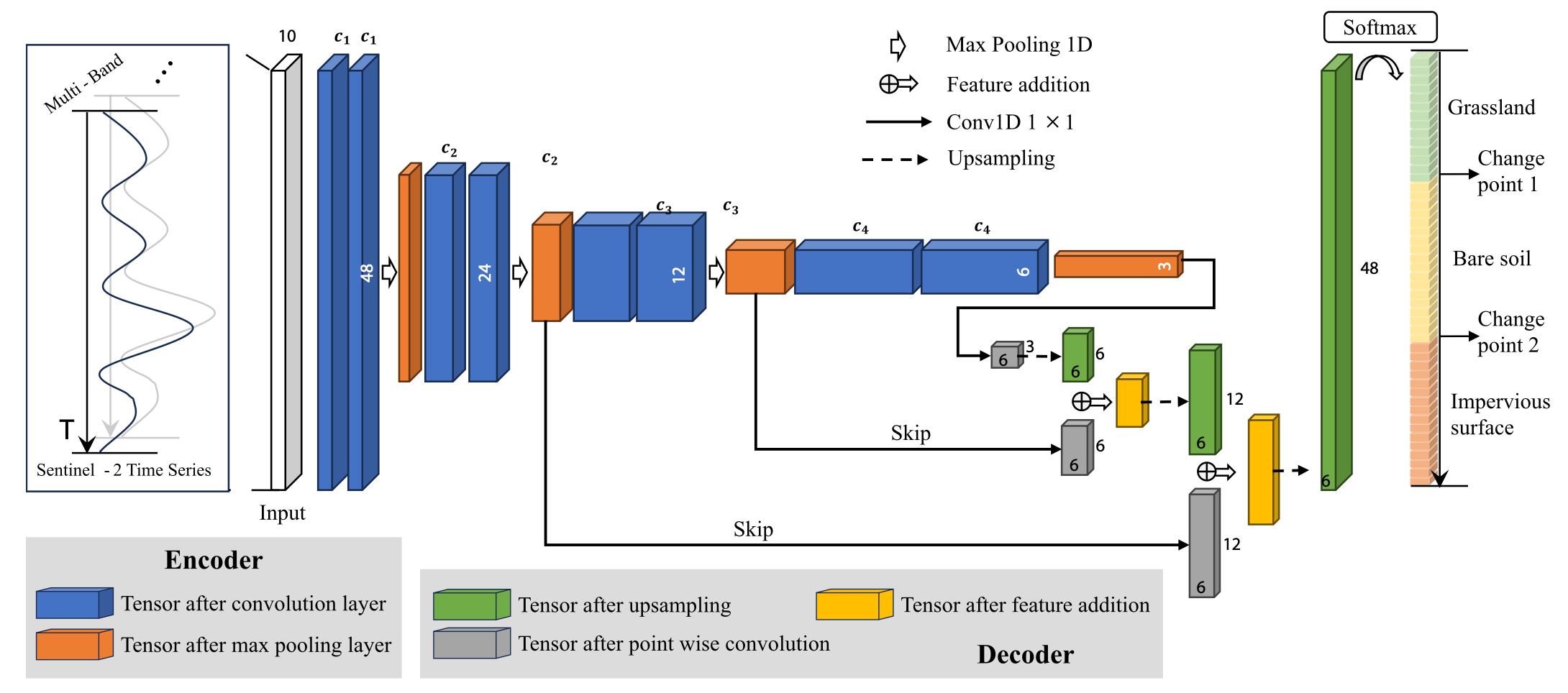
即 TSSCD 模型是一个一维全卷积网络,该模型采用卷积运算来提取每个时间点不同光谱波段之间的相关特征,从而学习它们与土地覆盖的映射,进而实现端到端的土地覆被变化检测和分类.

具体细节可阅读原文献.该方法在中国各区域的城市都展现了非常好的精度,并展现出非常好的迁移能力.

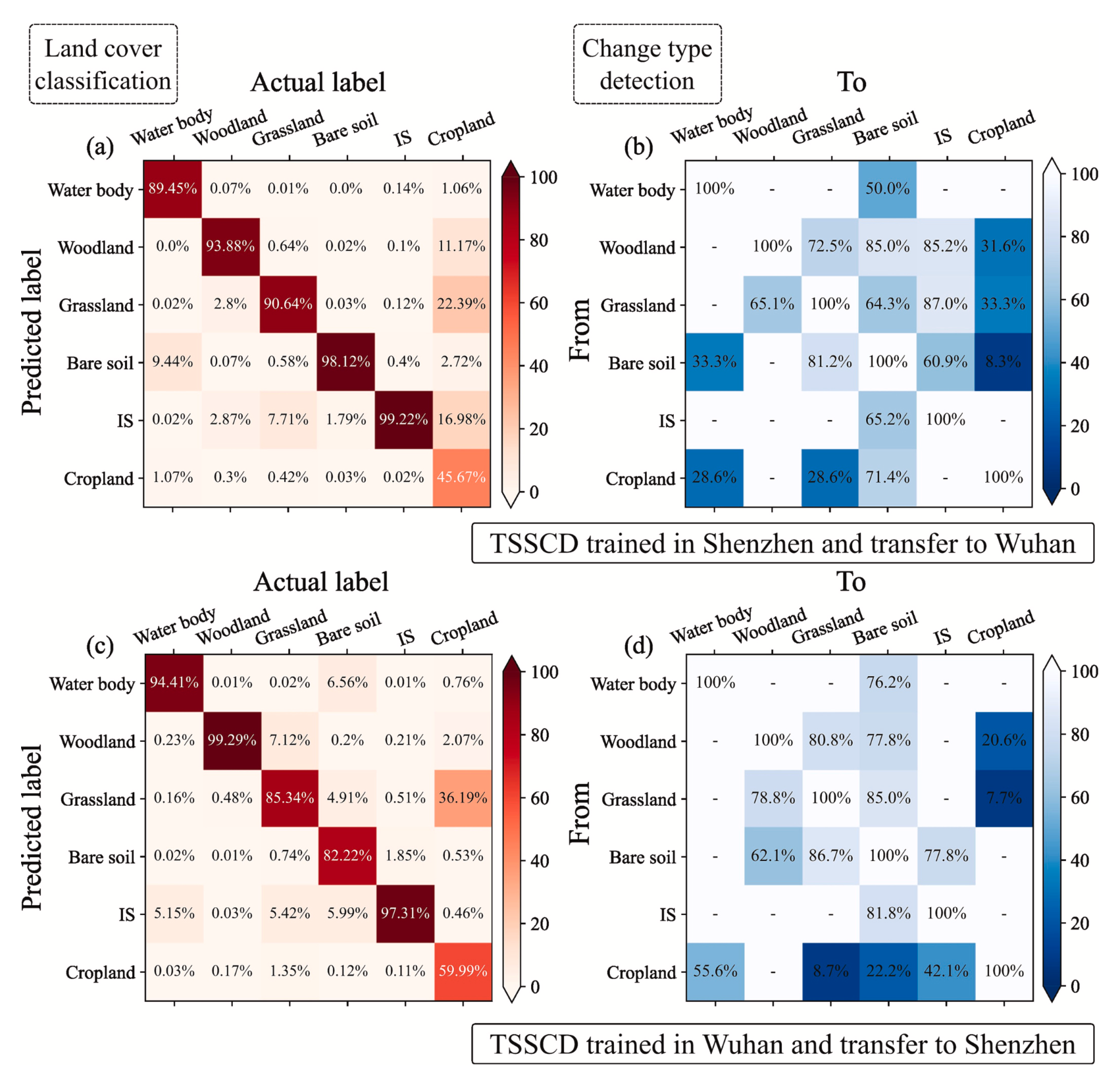
参考资料

  • Chen, T.-L., Chiu, H.-W., & Lin, Y.-F. (2020). How do east and southeast asian cities differ from western cities? A systematic review of the urban form characteristics. Sustainability, 12(6), 2423. https://doi.org/10.3390/su12062423
  • Dalal, N., & Triggs, B. (2005). Histograms of oriented gradients for human detection. 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), 1, 886–893. https://doi.org/10.1109/CVPR.2005.177
  • Guang-Bin Huang, Qin-Yu Zhu, & Chee-Kheong Siew. (2004). Extreme learning machine: A new learning scheme of feedforward neural networks. 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No.04CH37541), 2, 985–990. https://doi.org/10.1109/IJCNN.2004.1380068
  • He, H., Yan, J., Liang, D., Sun, Z., Li, J., & Wang, L. (2024). Time-series land cover change detection using deep learning-based temporal semantic segmentation. Remote Sensing of Environment, 305, 114101. https://doi.org/10.1016/j.rse.2024.114101
  • Long, J., Shelhamer, E., & Darrell, T. (不详). Fully convolutional networks for semantic segmentation.
  • Notarangelo, N. M., Mazzariello, A., Albano, R., & Sole, A. (2021). Comparing three machine learning techniques for building extraction from a digital surface model. Applied Sciences, 11(13), 6072. https://doi.org/10.3390/app11136072
  • Rottensteiner, F., Sohn, G., Gerke, M., & Wegner, J. D. (不详). Working group III / 4—3D scene analysis.
  • https://www.cnblogs.com/sixuwuxian/p/16757254.html
  • https://medium.com/ai反斗城/反捲積-deconvolution-上採樣-unsampling-與上池化-unpooling-差異-feee4db49a00
  • https://www.zywvvd.com/notes/study/image-processing/feature-extraction/hog/hog/
  • https://www.cnblogs.com/gujiangtaoFuture/articles/12177870.html