空间统计初体验---用统计魔法探索班级座位聚集规律
空间统计初体验:探索班级座位聚集规律
问题背景
空间统计的老师统计了本课程所有学生每次上课的座位分布发给我们进行课程实验,原始数据是一个座位统计表,包含了两个教学班109位同学7次上课的作为数据.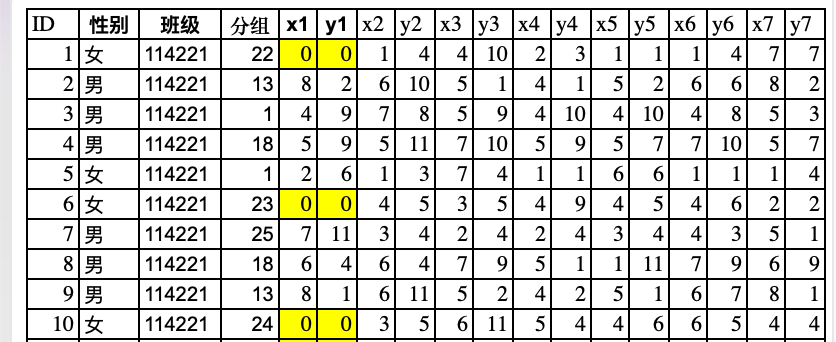 
其中\((x_i,y_i)\)表示表示该次课\(ID\)为\(i\)同学坐在第\(x_i\)行第\(y_i\)列的座位上(以教室左上角的座位为第\(1\)行第\(1\)列). 由于武汉开学返校时期的冻雨灾害造成的列车停运,第一节课有部分同学缺课(模拟数据污染).
本次实验使用matlab,想要探索的问题是: 1. 班级中有哪些同学倾向于聚集在一起. 2. 班级的座位分布是否在分组,班级和性别属性上存在聚集效应.
实验方法
构造统计量
针对想要探讨的问题,核心是如何度量两个同学之间座位选择的相关程度.统计班级中任意两个同学的上课座位相近程度的方式是构造空间邻接矩阵转换为特征空间上的距离.
两个同学之间座位选择的相关程度由上课座位的相近程度和座位变化的相似程度决定.
此处我选取两个指标衡量这一相关程度.
上课座位的空间距离度量
考虑到教室座位的构造: 教室共10列9行,其中3,4列之间与8,9列之间存在两条走廊,很明显跨越走廊的位置相邻与同一列组中的位置相邻程度不同.记原数据位置矩阵为\((X_0,Y_0)\),修正后位置矩阵\((X,Y)\)中\(ID\)为\(i\)的同学的座位坐标为:
\[ X(i) = X_0(i), Y(i) = \begin{cases} Y_0(i) &, 1 \leq Y_0(i) \leq 3 \\ Y_0(i)+1 &, 4\leq Y_0(i) \leq 8 \\ Y_0(i)+2 &, 9 \leq Y_0(i) \leq 11 \\ \end{cases} \]
则记\(ID\)为\(i\)的同学和\(ID\)为\(j\)的同学该次课的近邻多边形为:
\[ d_{i,j} = \begin{cases} 3 ,& X(i) = X(j),|Y(i) - Y(j)| =1 \\ 1 ,& X(i) = X(j),|Y(i) - Y(j)| =2 or\\ & Y(i) = Y(j),|X(i) - X(j)| =1 \\ 0 ,& \text{otherwise} \end{cases} \]
这样的构造还有一个巧妙的作用: 记\(c_i = \sum _{j=1}^{n}d_{i,j}\),则\(C_i\)越大说明该同学约倾向于坐中间的座位而非靠边或靠走廊的座位.下图说明不同位置的\(c_i\)取值.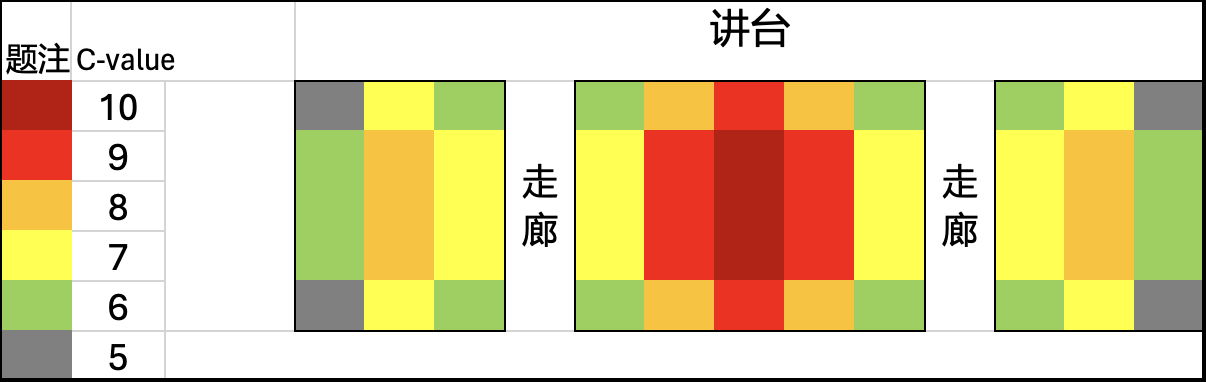 
则两个同学的总体上课座位相近程度\(D_{i,j} = \sum_{k=1}^7 d_{i,j}^{(k)}\),某一同学对中间座位的选择倾向度\(C_i = \frac{\sum_{k=1}^{time}c_{i}^{(k)}}{time}\),其中\(time\)表示该同学到课次数.
座位变化相似程度度量
座位变化的相似程度即为两个同学座位变化的一致程度,可以用两个同学座位变化路径差异程度的倒数表示..记\(ID\)为\(i\)的同学座位变化特征向量为: \[ \vec{v}_i = [\Delta x_1,\Delta x_2,\dots,\Delta x_{n-1},\Delta y_1,\Delta y_2,\dots \Delta y_{n-1}]; \] 其中\(\Delta y_i = y_{i+1} - y_{i}\),\(\Delta x_i = x_{i+1} - x_{i}\),\(n=7\). 则两个同学座位变化差异程度\(u_{i,j} = |\vec{v}_i - \vec{v}_j|\)
连接强度邻接矩阵构建
综上,记位置选择的相关程度为连接强度,则\(ID\)为\(i\)和\(ID\)为\(j\)的同学的连接强度\(A_{i,j} = \frac{D_{i,j}}{u_{i,j}}\).构建邻接矩阵如下: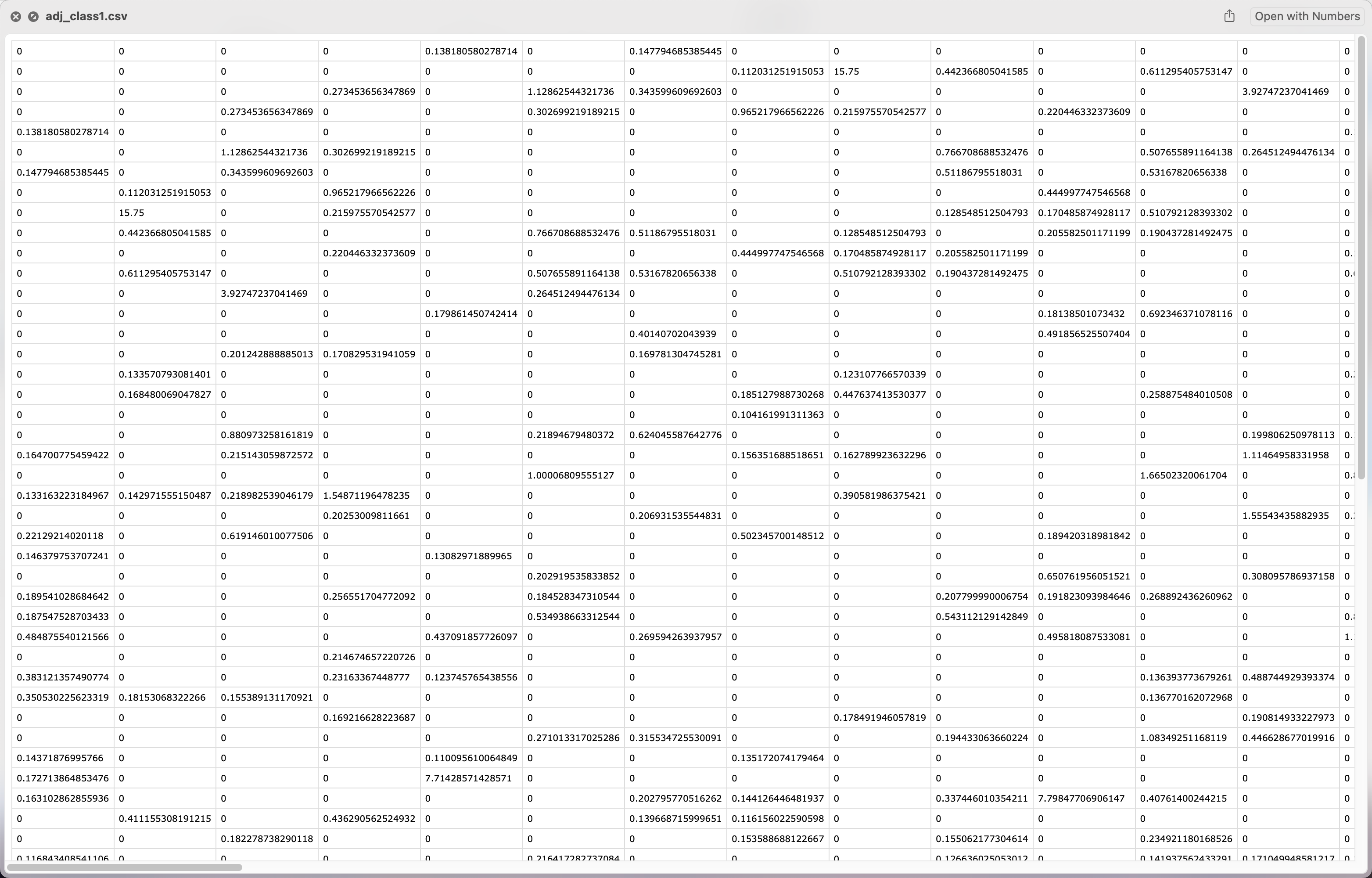 
蒙特卡洛法模拟随机模式
由于该统计量的构造较为复杂,难以直接计算其期望值,故采用蒙特卡洛法模拟随机模式.构建方式是根据原始数据中的座位分布在每一天的每一个位置上重新随机分配一位同学,这样既可以保持座位总体分布形态不变又进行了一个随机过程.
班级群体集聚形态分析
探索性空间分析
由空间邻接矩阵可画出班级内连接强度的拓扑关系.但是,我们希望找到的是强度较高的座位连接关系,即是因为关系较近而主观上倾向于坐在一起的聚集关系.因此需要找到一个合理的连接强度阈值用于判定该连接是偶然产生还是受主观倾向性影响.首先枚举连接强度阈值进行探索性空间分析.下图以教学班1举例: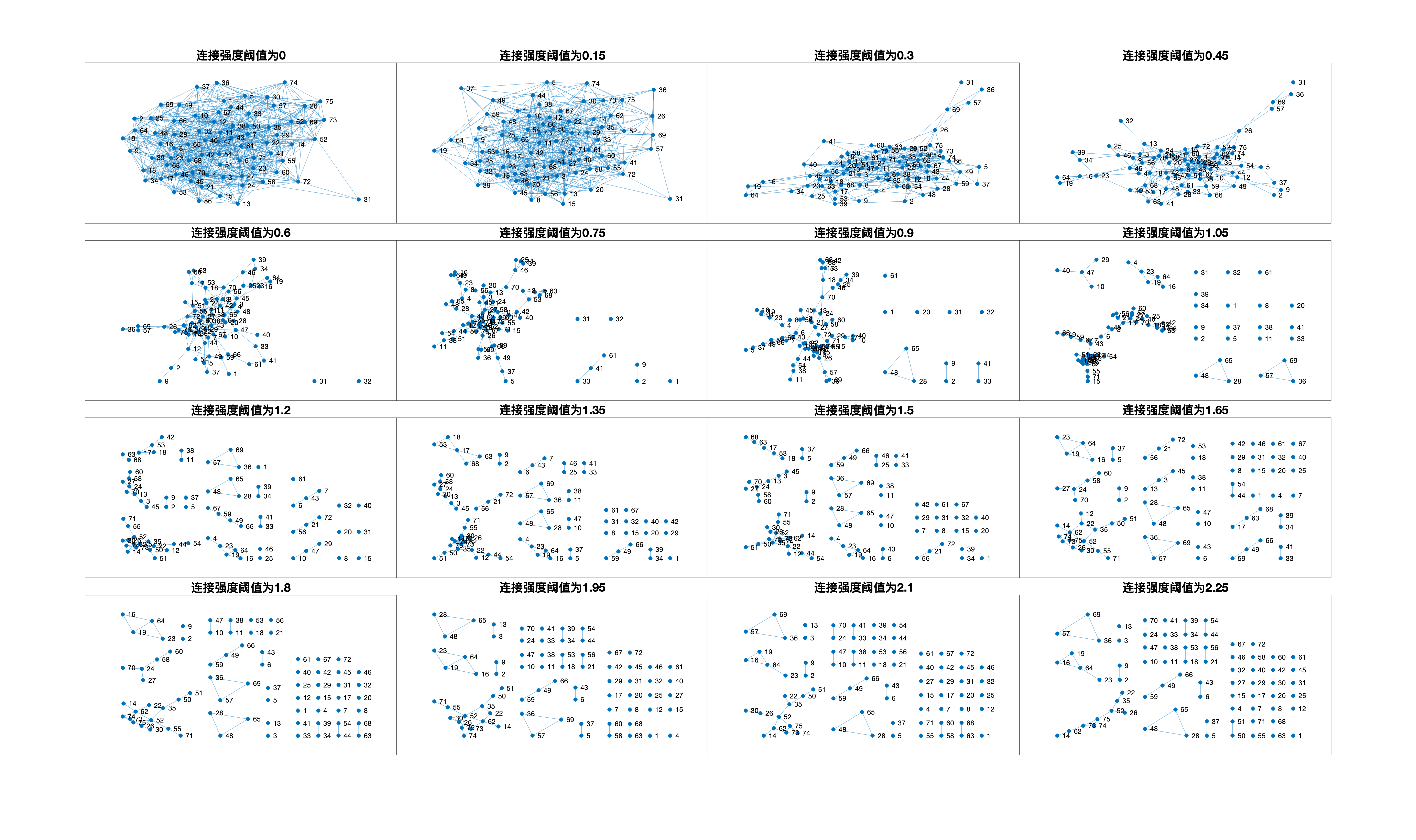 
可以发现合理的阈值应当落在1.2到2.2之间,以下采取一些分析工具推测出一个合理阈值.
合理阈值推测
一个合理的阈值应当是高于该阈值的连接强度是受主观性影响,低于该阈值的连接强度是偶然发生的.那么首先要确定的问题是哪些同学具有座位聚集选择的意愿. 不难意识到,具有座位聚集选择意愿的同学应当与一些同学具有较强的连接强度,而没有座位聚集选择意愿的同学应当与任何同学都没有较强的连接强度.因此座位连接向量\(\vec{a}_i = [A_{i1},A_{i2},\dots A_{in}]\)的均方根RMS可以衡量该同学的聚集选择意愿强度. 1
其实这个主观意愿的表述并不是很明确,因为两人之间的连接强度高可能是因为被选择(笑),不过这不是统计应该考虑的问题.
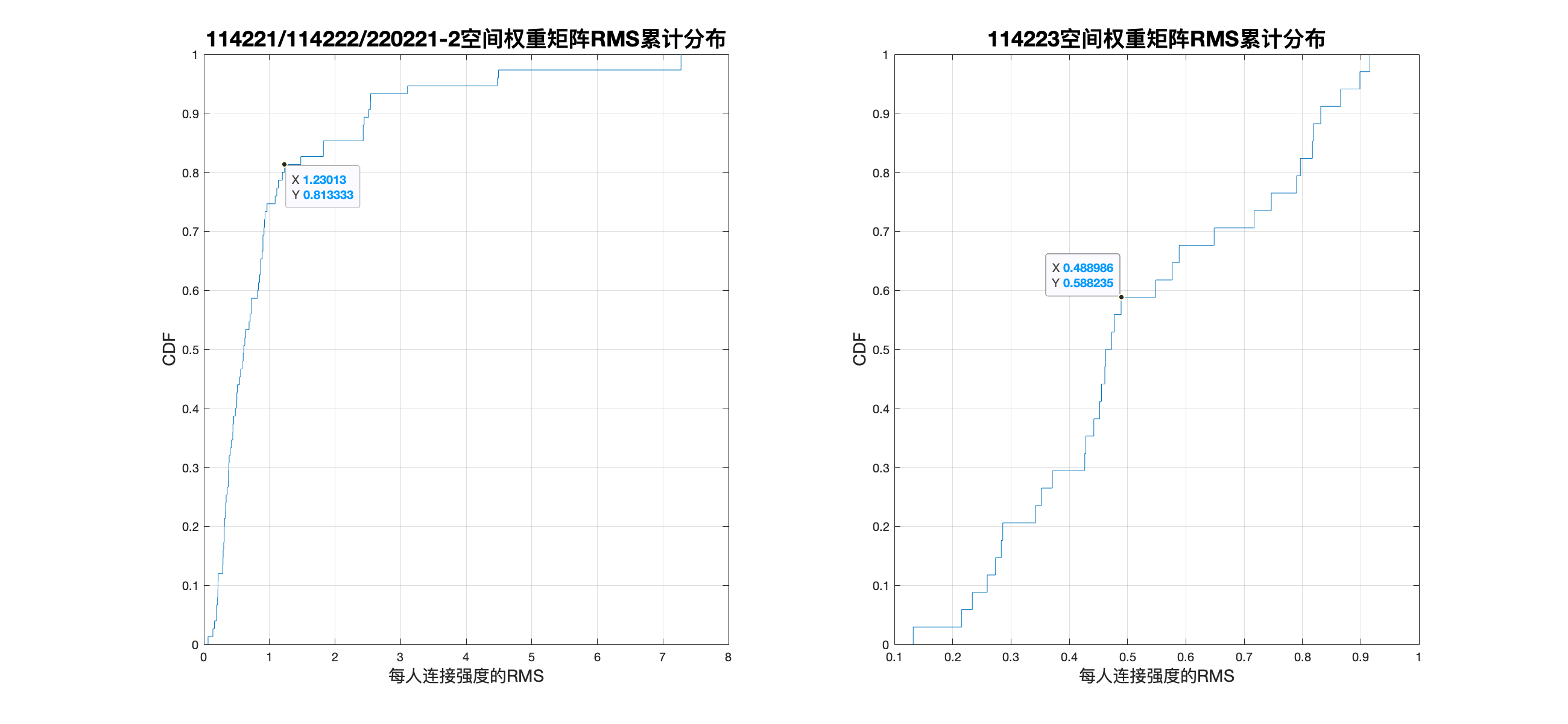在此基础上,我们考察这些有选择意愿同学的连接强度CDF得到: 
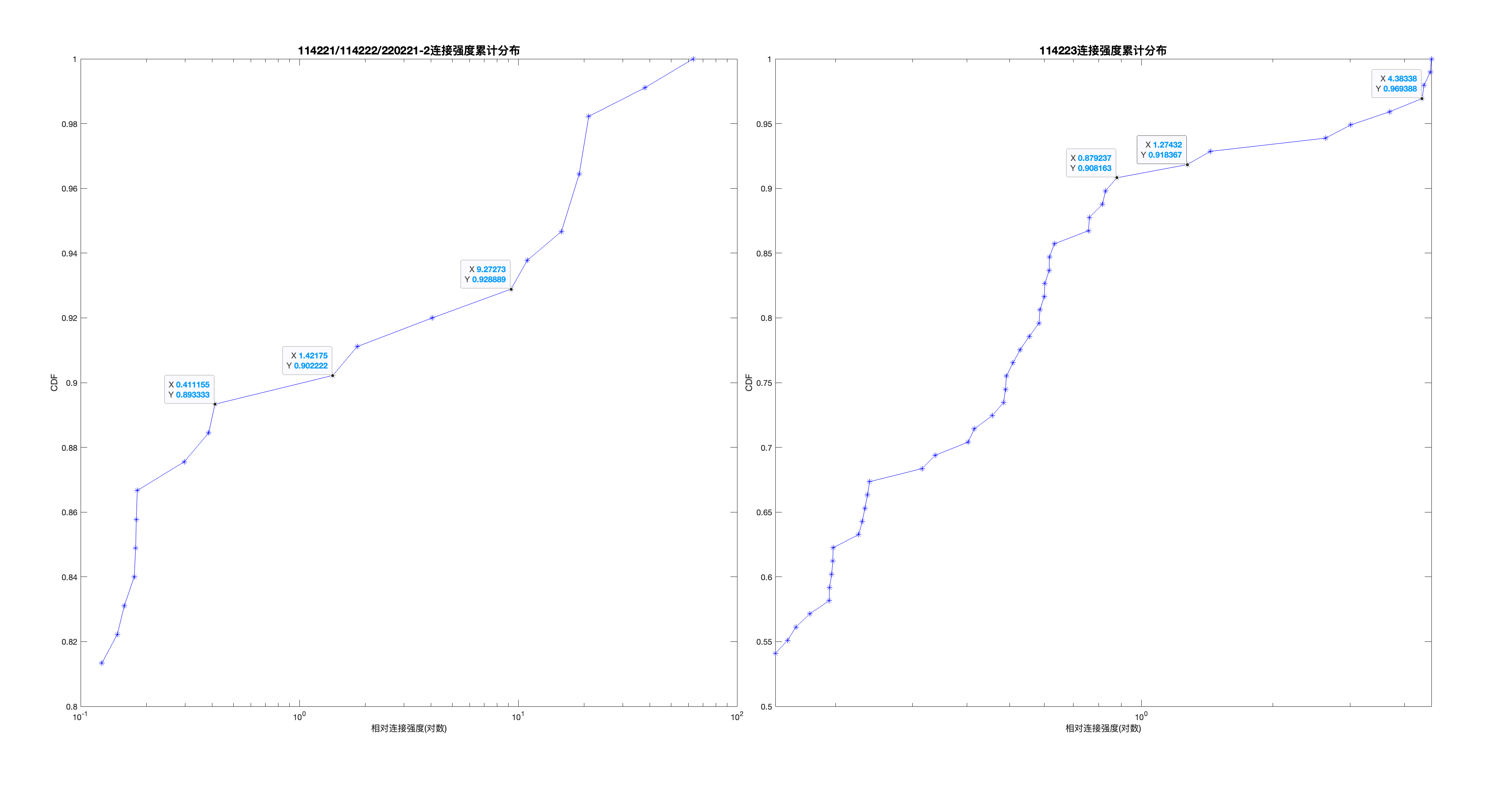CDF中第一个快速上升段的含义是随机产生的座位相关,故截取快速上升段的终点作为区分偶然和受主观倾向影响的座位选择的阈值.教学班1连接强度阈值设置为1.42,教学班1连接强度阈值为0.87.得到聚类结果如下: 
其中连线的明度越高代表连接强度越强. 从直觉上看这算是一个比较不错的结果,男生和男生更愿意坐一起,女生和女生更愿意坐一起,而在班级上没有呈现明显的聚集.同时也反映出三种聚集模式: 1. 无相邻选座主观倾向. 表现为孤立的点与其他同学连接强度较弱. 2. 朋友群体选座倾向. 表现为2~5名同学之间的选座具有明显的聚集模式. 3. 座位稳定型选座倾向. 表现为具有较长的关系链或较大型的关系网.主要由于该部分同学位置变动很小产生的相对固定的座位模式,从而呈现出相邻倾向.
可以发现教学班1(114221/114222/220221-2)的第三种聚集模式相较于教学班2(114223)具有更大的直径和更大连接强度,这表明由于人数差异(教学班1共75人,教学班2共34人),教学班1的同学的座位选择更受限,从而位置更加固定.
班级座位聚集效应分析
构造统计量假设检验
要检验班级中座位是否关于班级,性别和分组聚集分布,首先需要确定待检验的统计量和IRP/CSR过程产生的模式的统计量如何. 此处将群体内相互之间的平均连接强度作为统计量,即同学集合\(D\)的聚集统计量\(S_D\)为:
\[ S_D = \frac{\sum_{i,j \in D}A_{i,j}}{|D|} \cdot \sqrt{|D|} = \bar{A_D} \cdot \sqrt{|D|}= \frac{\sum_{i,j \in D}A_{i,j}}{\sqrt{|D|}} \]
其中在\(\bar{A_D}\)的基础上再乘\(\sqrt{|D|}\)的原因是\(A_{i,j}\)中只被\(i\)和\(j\)位置时相邻,而随着群体数量增加,使得群体中有较多人同时相邻是不可能的,故采用该方法修正. 然后,采用蒙特卡罗法模拟10000次上课座位情况,可以发现当群体规模较大时,统计量\(S\)较好地服从正态分布.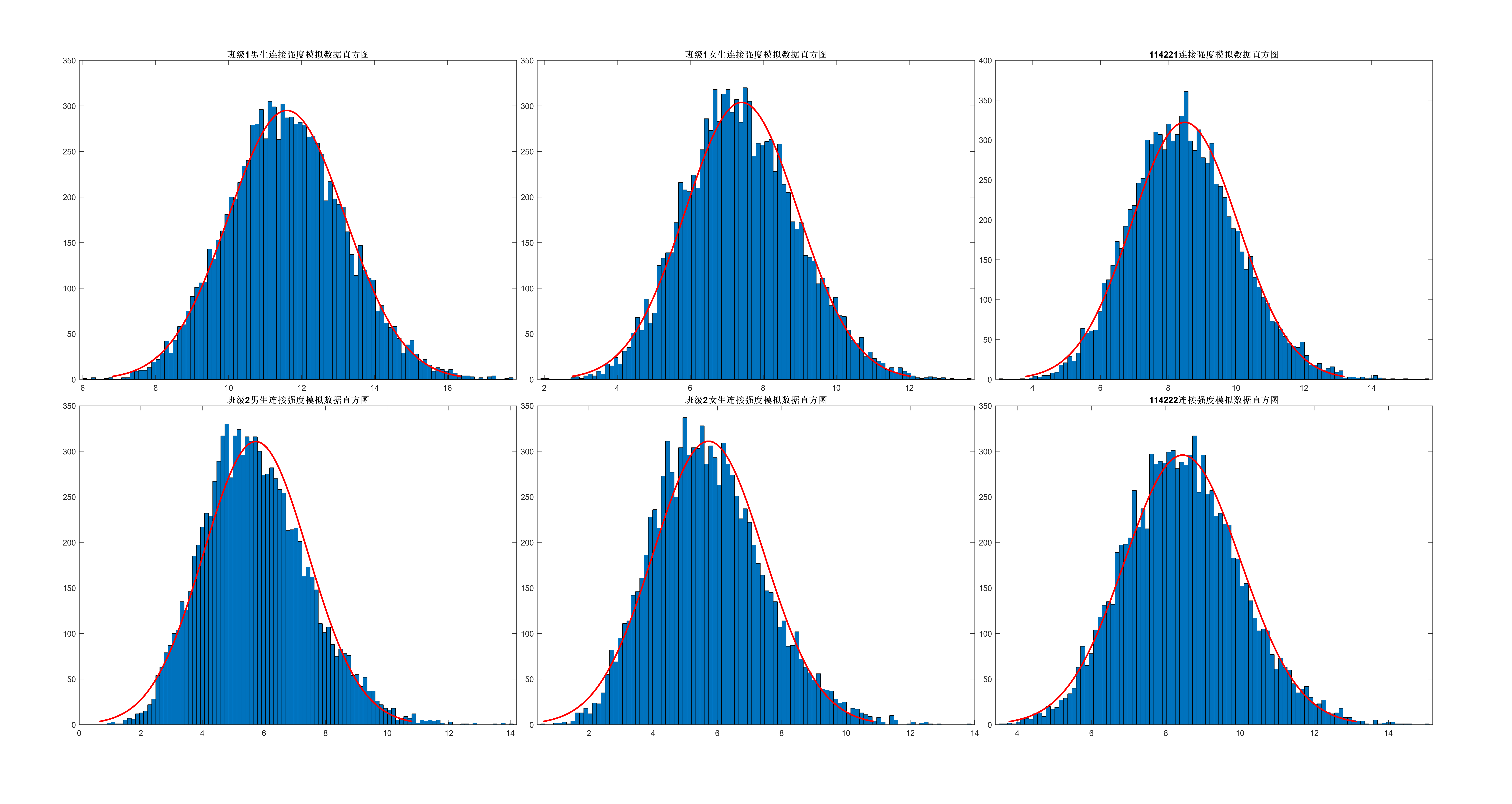 
而由于未来技术学院同学选课人数为5人,因此在IRP/CSR过程中\(S\)均趋近于0,对比下表数据可以轻易得出未来技术学院同学倾向于聚集分布. 
在此处零假设是IRP/CSR过程产生的群体内平均连接强度与实际过程产生的群体内平均连接强度均值相等,备则假设则是不相等对于性别和班级数据,由于数据量太小,因此使用蒙特卡洛生成的1000次数据对其进行z检验,而对于分组数据则可使用双样本t检验.结果如下.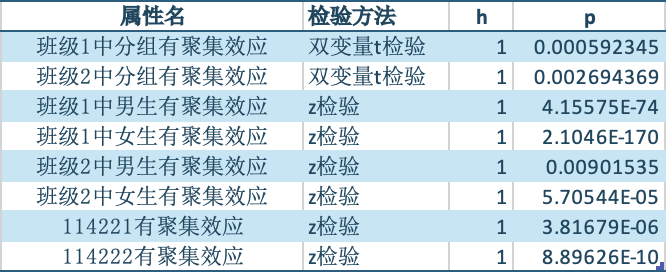 
可以发现在每一个属性上都存在聚集效应.
对该模式中一阶效应的分析
实际上上述分析忽略一个一个重要问题: 该模式是否存在一阶效应? 在分析聚集这一二阶效应前,是否需要处理其非齐次性?
事实上此处存在两个可能存在的一阶效应: 1. 靠近走廊/靠边的座位被选择概率是否和靠近中间的座位的被选择概率相同? 2. 前排座位是否比后排座位更具吸引力?
这两个问题是真实存在的: 一些同学更愿意坐在前排而另一些更愿意坐在后排,一些同学喜欢靠边而另一些喜欢坐在中间.进而拥有相同位置偏好的同学之间将会天然地拥有更大的连接强度.
那么,我们是否要据此对此处的IRP/CSR过程进行修正呢,如在模拟时一个同学选择靠近其在实际中座位质心距离近的座位的概率更大? 这个问题我想了一段时间,由于这个程序很难实现,也许首先需要明确的是这样的一阶效应是否会对聚集结果产生明显的影响? 为此,我们仿照上文,检查由蒙特卡洛法生成的选座中每个同学连接强度的均方根,画出箱线图: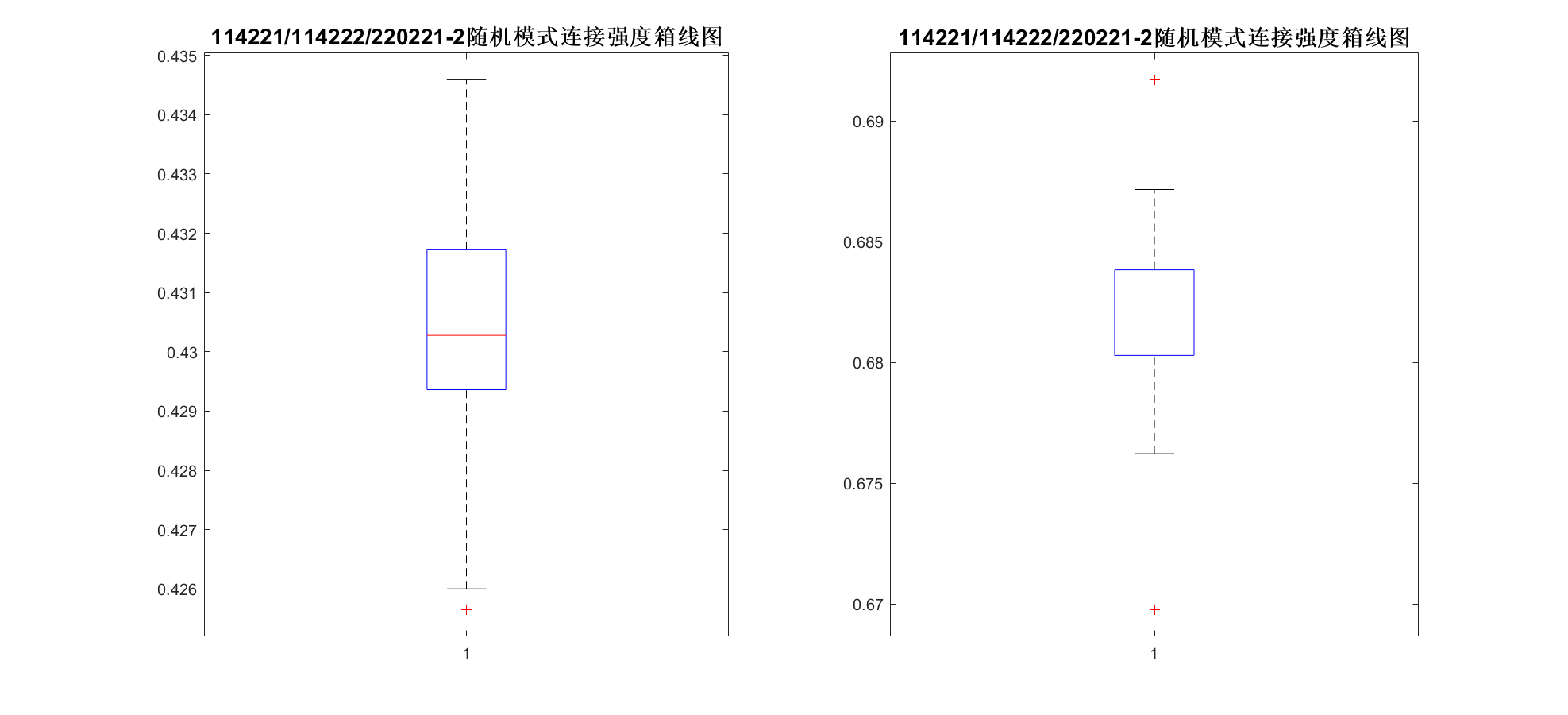 
对比上文实际连接强度RMS的CDF图像可以发现,由随机模式产生的连接强度与实际中我们认为的由于随机过程产生的连接强度非常接近.在教学班1中实际观测值为0.412,模拟值中位数约为0.430;在教学班2中实际观测值为0.880,模拟值中位数约为0.681.
同样的,计算选座倾向度\(C_i\)的方差,教学班1的75人选座倾向度方差仅为1.5521,教学班2的34人选座倾向度方差仅为2.5355,比值为1.634.模拟结果中教学班1选座倾向度\(C_i\)方差为\(4.496 \times 10^{-4}\),教学班2方差为\(8.394 \times 10^{-4}\),比值为1.867且均接近理论值0(而由于边界效应的存在达到0是不可能的).说明实际中选座倾向度方差的差异主要是由于人数差异导致的. 因此上述考虑的两个一阶效应均对聚类结果没有影响.
后记
这篇分析真的用了非常多的心思,同时也有非常大的收获,真正体验了一把从0到1的严密的统计分析,并且对点模式分析中可能遇到的各类问题有了深刻地多的理解.甚至一下都想不到这篇分析有什么不足之处.
心情很激动٩(๑>◡<๑)۶